Progressive and Stationary Waves

In a sonometer wire the tension is maintained by suspending a 50.7 kg mass from the free end of the wire. The suspended mass has volume of 0.0075m^​3. The fundamental frequency of the wire is 260Hz. Find the new fundamental frequency if the suspended mass is completely submerged in water

A string of length $1 \mathrm{m}$ and mass $2\times {10}^{-5} \mathrm{kg}$ is under tension $T$. When the string vibrates, two successive harmonics are found to occur at frequencies $750 \mathrm{Hz}$ and $1000 \mathrm{Hz}$. The value of tension $T$ is _____ newton.

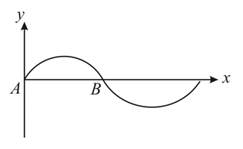
A part of snapshot of progressive wave propagating in a uniform string is shown in figure-$1$ and a snapshot of standing wave in a string (identical to case-$1$) is shown in figure $-2$.
The amplitude, frequency and wave length of waves in both cases is same. $A$ and $B$ (anti node) are material cross-section on strings. At the instant shown both $A\&B$ are at their respective maximum displacement. $dE$ represents wave energy of small element of length $dx$.

A disc placed on a frictionless horizontal plank is rotating with a constant angular velocity $\omega$ about its central vertical axis. Now the plank is made to move with a constant acceleration $\alpha$ on a straight path. If you assume initial location of the centre of disc as origin, direction of motion of the plank in negative $y$-axis of the coordinate system attached with the plank, which of the following equations represent trajectroy of instantaneous centre of rotation of the disc.

The tension in a stretched string fixed at both ends is changed by $2\%,$ The fundamental frequency is found to get changed by $15 \mathrm{Hz}.$ Select the correct statement(s):

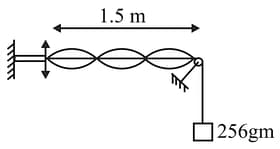
A string is stretched between a pulley and a wave generator consisting of a plate vibrating up and down with small amplitude and frequency $120 \mathrm{Hz}$. The standing wave pattern has $4$ nodes as shown. What should be the load (in gm) we want a standing wave with $5$ nodes.

The equation of a wave on a string of linear mass density $0.04 \mathrm{kg} {\mathrm{m}}^{-1}$ is given by,  $y=0.02\left(\mathrm{m}\right)\sin \left[2\mathrm{\pi }\left(\frac{t}{0.04\left(\mathrm{s}\right)}-\frac{x}{0.50\left(\mathrm{m}\right)}\right)\right]$.

The tension in the string is $n\times {10}^{-2 }\mathrm{N}$. Write the value of $n$.

A string of length $1.5 \mathrm{m}$ with its two ends clamped is vibrating in the fundamental mode. The amplitude at the centre of the string is $4 \mathrm{mm}$. The minimum distance between the two points having amplitude of $2 \mathrm{mm}$ is:

One end of a uniform string is attached to an oscillator which is oscillating along $y$ axis according to the law $y=\left\{\begin{array}{cc}t-\left[t\right]& 2n<t<2n+1\\ 0& 2n+1<t<2n+2\end{array}\right.$
Where $y$ is in meters, $t$ is in seconds and $n=0,1,2,3\dots .$ Other end of string is fixed to rigid wall. Tension in the string is $25 \mathrm{N}$, mass of string is $10 \mathrm{kg}$ and length is $10 \mathrm{m}$ Let oscillator be placed at origin and wall is at $x=10$ then answer following question. {Assume gravity free space and no damping}

The tension in a stretched string fixed at both ends is increased by $2\%$, the fundamental frequency is found to get increased by $15 \mathrm{Hz}$. Select the correct statement(s):

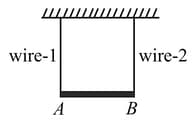
A rod of length$0.3 \mathrm{m}$ having variable linear mass density from $A$ to $B$ as $\lambda ={\lambda }_{0}x(\mathrm{x}$ is distance from $A$ in meter), where ${\lambda }_0=100 {\mathrm{kgm}}^{-2}$ is suspended by two light wires of same length. Ratio of linear mass density of wire$- 1$ and wire$- 2$ is $2: 9$

.

Then which of the following is/are CORRECT:

A long wire $PQR$ is made by joining two wires $PQ$ and $QR$ of equal radii. $PQ$ has a length $4.8 \mathrm{m}$ and mass $0.06 \mathrm{kg}$. $QR$ has length $2.56 \mathrm{m}$ and mass $0.2 \mathrm{kg}$. The wire $PQR$ is under a tension of $80 \mathrm{N}$. A sinusoidal wave pulse of amplitude $3.5 \mathrm{cm}$ is sent along the wire $PQ$ from the end $P$. No power is dissipated during the propagation of wave pulse. Find amplitude (in $\mathrm{mm}$) of reflected pulse from junction $Q$.

A string will break apart if it is placed under too much tensile stress. One type of steel has density. ${\rho }_{\mathrm{steel} }={10}^4 \mathrm{kg} {\mathrm{m}}^{-3}$ and breaking stress $\alpha =9\times {10}^8 \mathrm{N} {\mathrm{m}}^{-2}$. We make a guitar string from $\left(4\pi \right)$ gram of this type of steel. It should be able to withstand $\left(900\pi \right)N$ without breaking. What is highest possible fundamental frequency (in $\mathrm{Hz}$ ) of standing waves on the string if the entire length of the string vibrates?

A transverse wave is travelling on a string with speed $v$. The shape of string at $t=1\sec$ is given by $y=\frac{5}{x^2+6x+9}$ and at $t=2sec$, it is given by $y=\frac{5}{x^2+12x+36}$, then fill the value of $\left(v+c\right)$, where $c$ is number that denotes the direction of motion of wave ($+1$ for positive $x$-direction and $-1$ for $-vex$-direction). (Consider SI units through out)

Choose correct statements

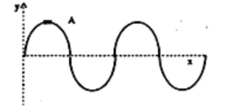
Three simple harmonic waves, identical in frequency $n$ and amplitude A moving in the same direction are superimposed in air in such a way, that the first, second and the third wave have the phase angles $\varphi ,\varphi +\left(\frac{\pi }{2}\right)$ and $\left(\varphi +\pi \right)$, respectively at a given point $P$ in the superposition. Then as the waves progress, the superposition will result in

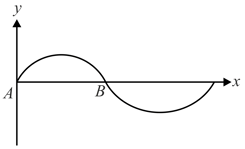
A part of snapshot of progressive wave propagating in a uniform string is shown in figure-$1$ and a snapshot of standing wave in a string (identical to case-$1$) is shown in figure $-2$. The amplitude, frequency and wave length of waves in both cases is same. $A$ and $B$ (anti node) are fixed cross-section on strings. At the instant shown both $A$ & $B$ are at their respective maximum displacement. '$E$' represents energy of wave.

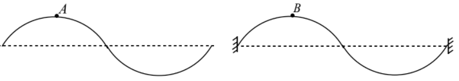
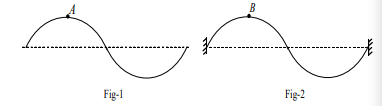
A part of snapshot of progressive wave propagating in a uniform string is shown in figure-$1$ and a snapshot of standing wave in a string (identical to case-$1$) is shown in figure $-2$.
The amplitude, frequency and wave length of waves in both cases is same. $A$ and $B$ (anti node) are fixed cross-section on strings. At the instant shown both $A\&B$ are at their respective maximum displacement. '$E$' represents energy of wave.

A plane progressive transversal mechanical wave is advanced in a medium along the $+x$-axis in the ground frame of reference is represented by the equation $y=A\sin \left(\omega t-kx\right)$ then which of the following statements are correct?

The equation of a one dimensional transverse wave is given by $\psi =\left({10}^{-3}\right)\sin \pi \left(10t-3x-2y+z\right)$ where $x,y$ and $\psi$ are expressed in meter and $t$ in second Choose the correct option(s)